手把手教你Lambda式类型推导，C++老登都能看懂（2）

CAUTION

C++老登其实看不懂

NOTE

预备知识：你需要熟悉 Haskell 的基本语法，了解递归和高阶函数。例如，你应该能自己实现 zipWith、map 这样的函数。

对应代码：https://github.com/xiaoshihou514/xingli

引言

上回我们实现了类型推导的前两种情况（变量和抽象），但卡在了最复杂的应用情况上。我们需要想办法统一应用中函数和值的类型：

pp' ctx (Ap m n) = s2 . s1 $ (ctx1 `union` ctx3, a)
  where
    (ctx1, p1) = pp' ctx m
    (ctx2, p2) = pp' ctx1 n
    (a, ctx3) = next ctx2
    -- 关键步骤！
    s1 = unify p1 (p2 --> a)
    s2 = unifyctx (s1 ctx1) (s1 ctx3)

我们今天正是要“统一“p1和p2 --> a。

类型统一

如何“统一”两个类型呢？主偶算法认为，应当替换某个基本类型，让两个类型相等，举例来说：对于式子f x，f为类型A，x为类型B，需要统一A和B -> C，这里的替换规则就需要将A替换成B -> C，使得A = B -> C。

TIP

💡动手试一试：如何统一以下类型？

p1	p2 --> a
B -> C	A
A -> B	C -> D
A	A -> B

主偶算法将其定义如下：

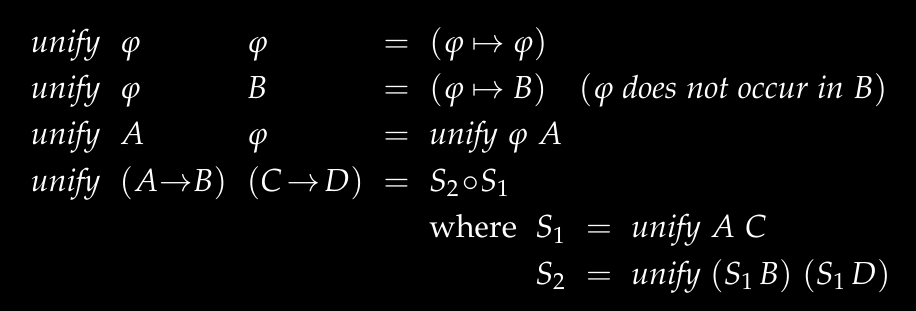
一共四种情况，这里phi代表基本类型（Int、String），A、B代表任意柯里类型（可能是复杂的箭头类型）。

• 两边都是简单类型且相等：不需要替换，本来就一样
• 左边简单类型，右边复杂类型：返回一个映射，把左边映射到右边。如果左边在右边的类型里出现，那么不能统一（如A不论如何替换A = A -> B都显然不成立）。
• 右边简单类型，左边复杂类型：同上。
• 左右都是箭头类型：首先递归尝试统一A和C，根据映射修改B、D，再尝试统一B、D，最终映射是两个映射的组合。

于是可以写得：

unify :: CurryType -> CurryType -> (CurryType -> CurryType)
unify left right
  -- 两边相等
  | (Phi p1) <- left, (Phi p2) <- right, p1 == p2 = id
  -- 左简单右复杂，且左式不能在右式出现
  | (Phi p) <- left, p `notOccur` right =
      -- 定义替换映射，替换所有p为right
      let subst ty = case ty of
            Phi _ -> if ty == left then right else ty
            Arrow a b -> Arrow (subst a) (subst b)
       in subst
  -- 左复杂右简单
  | (Phi _) <- right = unify right left
  -- 两边均复杂
  | (Arrow a b) <- left,
    (Arrow c d) <- right =
      let s1 = unify a c            -- 首先统一A、C
          s2 = unify (s1 b) (s1 d)  -- 根据替换修改B、D，然后统一
       in s2 . s1                   -- 组合两个映射
  | otherwise = error $ "Cannot unify " ++ prettyCT left ++ " and " ++ prettyCT right

定义notOccur如下：

notOccur :: Label -> CurryType -> Bool
notOccur p (Phi a) = p /= a
notOccur p (Arrow a b) = p `notOccur` a && p `notOccur` b

上下文统一

两边的上下文也可能冲突，考虑xy(xz)，两边x的类型显然不一样（y和z根据我们之前的逻辑不可能相等，那么两个x的输入类型就肯定不一样）。我们需要统一两个上下文对变量的描述。

统一上下文用到了之前定义的unify函数，意思是说，如果某变量x在两个上下文中均有定义，那么所有这样的x都需要被统一，而具有这样效果的映射是所有单个变量修正映射的组合。

这里的Haskell代码可能比较复杂，试试看能不能看懂吧！

unifyctx :: TypeCtx -> TypeCtx -> (PrincipalPair -> PrincipalPair)
unifyctx ctx1 ctx2 = liftPP $ foldr (.) id subs
  where
    subs = [unify a b | (x, a) <- Map.toList env1, b <- maybeToList $ Map.lookup x env2]
    env1 = env ctx1
    env2 = env ctx2

liftPP :: (CurryType -> CurryType) -> (PrincipalPair -> PrincipalPair)
liftPP f (TypeCtx env l, a) = (TypeCtx (Map.map f env) l, f a)

首先我们获取所有被二次定义的变量，并找出它们的修正映射：

env1 = env ctx1
env2 = env ctx2
subs = [unify a b |
    (x, a) <- Map.toList env1,
    -- <-并不能提取Maybe中的值，因此把它转成列表
    b <- maybeToList $ Map.lookup x env2
]

使用foldr组合所有映射：

foldr (.) id subs

我们现在得到的映射只能修正一个类型，为了能够将其应用于整个上下文，定义liftPP将其作用于所有上下文中的类型。

liftPP :: (CurryType -> CurryType) -> (PrincipalPair -> PrincipalPair)
liftPP f (TypeCtx env l, a) = (TypeCtx (Map.map f env) l, f a)

结束了...吗？

前文没写完的最后一种情况就可以补全了：

-- 只是lift了一下s1，别的一点没改
pp' ctx (Ap m n) = s2 . liftPP s1 $ (ctx1 `union` ctx3, a)
  where
    -- 首先递归推导函数
    (ctx1, p1) = pp' ctx m
    -- 递归推导输入
    (ctx2, p2) = pp' ctx1 n
    -- 统一两个类型
    (a, ctx3) = next ctx2
    s1 = unify p1 (p2 --> a)
    -- 统一上下文的类型
    s2 = unifyctx (s1 ctx1) (s1 ctx3)

举个具体例子：推导 (\x.x) y

1. 推导 (\x.x)：得到 {x: A}, 类型 A -> A
2. 推导 y：得到 {x: A, y: B}, 类型 B
3. 新类型变量：C
4. 统一 A->A 和 B->C：
   • 统一 A 和 B：把A映射到B
   • 统一 A 和 C：但A已经是B了，所以统一B和C，把B映射到C
   • 最终：A↦C, B↦C
5. 应用替换后：类型是 C，上下文是 {x: C, y: C}

那么到这其实就实现完了，下面是Haskell小课堂时间。

一点重构

注意到我们在unify里会直接报错，这其实不太好，因为我们在类型里宣称我们可以推导任意Lambda式的类型，但我们有时候却推不出来（可以尝试推导一下\x.(x x) \x.(x x)）。

在Haskell里，最简单的解决方案是返回一个Maybe，明确表示可能推不出类型：

unify :: CurryType -> CurryType -> Maybe (CurryType -> CurryType)
unify left right
  -- 前几个情况加一个Just即可
  | (Phi p1) <- left, (Phi p2) <- right, p1 == p2 = Just id
  | (Phi p) <- left, p `notOccur` right =
      let subst ty = case ty of
            Phi _ -> if ty == left then right else ty
            Arrow a b -> Arrow (subst a) (subst b)
       in Just subst
  | (Phi _) <- right = unify right left
  -- 这里用了do语法链式处理Maybe
  | (Arrow a b) <- left,
    (Arrow c d) <- right = do
      s1 <- unify a c           -- 如果失败，直接返回Nothing
      s2 <- unify (s1 b) (s1 d) -- 同上
      return $ s2 . s1          -- return = Just
  | otherwise = Nothing

pp :: Term -> PrincipalPair
pp :: Term -> Maybe PrincipalPair
pp = pp' emptyEnv
  where
    pp' :: TypeCtx -> Term -> PrincipalPair
    pp' :: TypeCtx -> Term -> Maybe PrincipalPair
    pp' = ...

这里我们使用了do语法，效果上来说，x <- ...会“解包”Maybe，如果是空的，直接返回空，否则将值取出来。由于next一定成功（不返回Maybe），因此用let语法表示不需要解包。最后的return相当于打包（Just一下，Maybe的Monad实现）。

还需要修改上层代码：

由于前三种情况一定成功，所以只需加一个Just满足类型约束即可。

pp' :: TypeCtx -> Term -> Maybe PrincipalPair
pp' ctx (V c) =
  let (a, ctx') = next ctx
   in (add c a ctx', a)
   in Just (add c a ctx', a)
pp' ctx (Ab x m) = do
  (ctx', p) <- pp' ctx m
  case env ctx' !? x of
    Just ty -> Just (ctx', ty --> p)
    Nothing ->
      let (a, ctx'') = next ctx'
      in (add x a ctx'', a --> p)
      in Just (add x a ctx'', a --> p)

最后一种情况，同样使用do语法处理：

pp' ctx (Ap m n) = s2 . liftPP s1 $ (ctx1 `union` ctx3, a)
  where
    (ctx1, p1) = pp' ctx m 
    (ctx2, p2) = pp' ctx1 n 
    (a, ctx3) = next ctx2 
    s1 = unify p1 (p2 --> a)
    s2 = unifyctx (s1 ctx1) (s1 ctx3)
pp' ctx (Ap m n) = do
  (ctx1, p1) <- pp' ctx m 
  (ctx2, p2) <- pp' ctx1 n 
  let (a, ctx3) = next ctx2 
  s1 <- unify p1 (p2 --> a)
  s2 <- unifyctx (apply s1 ctx1) (apply s1 ctx3)
  return $ s2 . liftPP s1 $ (ctx1 `union` ctx3, a)

最后我们需要修改一下unifyctx：

subs :: [Maybe (CurryType -> CurryType)]
unifyctx ctx1 ctx2 = liftPP . foldr (.) id subs 
unifyctx ctx1 ctx2 = liftPP . foldr (.) id <$> sequence subs 

这里<$>只是fmap的另一种写法（回忆一下，Maybe对应的fmap是什么效果？）

f <$> maybe = fmap f maybe

sequence比较复杂，首先看一下它的类型：

sequence :: (Traversable t, Monad m) => t (m a) -> m (t a)
-- 上述调用的具体类型：t = [a], m = Maybe
sequence :: [Maybe (... -> ...)] -> Maybe [... -> ...]

具体来说，就是如果列表里有一个Nothing（失败了），那就整体返回Nothing（整体失败），反之则返回Just [...]。这正是我们想要的。

动动手，动动脑

问题1 手动推导 (\x.\y.x) (\z.z) 的类型：

• 按步骤写出每个推导阶段的上下文和类型
• 每次类型统一的替换映射是什么？

问题2 为什么 \x.(x x) 无法推导出类型？尝试手动推导并找出问题所在。

问题3 思考题：我们无法推导所有不动点组合子（因为它们都有自应用，A和A -> A没法统一），我们依赖不动点组合子来表达递归，所以我们现在还没法推导递归函数的类型。可以怎么解决这个问题？

---

恭喜！你现在已经理解了一个完整的类型推导算法。

完整代码参考：GitHub仓库

当然，这只是最简单的类型系统 :)

如果你想知道如何推导更复杂的情况（如何推导where？如何推导递归函数？），可以看我的下一篇博客。接下来我们会逐步引入更多概念，让Lambda式逐渐可以表达Haskell中的任意表达式。