手把手教你Lambda式类型推导，C++老登都能看懂（1）

CAUTION

C++老登其实看不懂

NOTE

预备知识：你需要熟悉 Haskell 的基本语法，了解递归和高阶函数。例如，你应该能自己实现 zipWith、map 这样的函数。

对应代码：https://github.com/xiaoshihou514/xingli

引言

在函数式编程的世界里，Lambda演算是一切的基础。这套看似简单的数学体系——只有变量、函数抽象和函数应用三条规则——却拥有与图灵机等价的表达能力，是整个函数式编程的理论基石。

当你写下Haskell中的匿名函数 \x -> x + 1，或者Scala中的 (x: Int) => x + 1，你其实就在使用Lambda式的现代变体。这些"函数值"让函数成为一等公民，可以像普通值一样传递和组合。

但为什么我们需要关心类型推导呢？

在Haskell中，你写下 map (\x -> x + 1)，编译器能自动推断出整个表达式的类型是 [Int] -> [Int]，而不需要你显式标注每个中间结果的类型。这种魔法的背后，正是基于Lambda式的类型推导算法。

理解类型推导，能让你：

• 🎯 深入理解Haskell类型系统：不再对类型错误信息感到困惑
• 💡 培养类型思维：真正理解类型，让类型为你所用
• 🧠 掌握现代语言设计思想：TypeScript、Rust等语言的类型系统都借鉴了这些理论

接下来，我们将手把手实现一个完整的类型推导算法，让你亲身体验Haskell编译器背后的奥秘。

基础定义

首先，定义Lambda式和类型。

Lambda式

我们先来看几个例子：

• x（一个变量）
• \x.x（恒等函数 id）
• \x.\y.x（总是返回第一个参数的函数，left）
• (\x.\y.x) (\x.x) = left id

Lambda 表达式的语法由以下三条规则递归定义：

Lambda式有以下递归定义（太长不看）：

• 变量：x，y，z...
• 抽象：\x.M，M为Lambda式（相当于Haskell中的匿名函数）
• 应用：M N，M、N为Lambda式（相当于函数调用）

类型

例：A、A -> B、(A -> B) -> C、(A -> B) -> A -> B

这里我们使用最简单的柯里类型系统，即：或基本类型（Int、String等，这篇博客统一用A、B）、或箭头类型类型 -> 类型（与Haskell类型相同）

在Haskell中的表示

data Term = V Char          -- 变量，如 'x'
          | Ab Char Term    -- 抽象，如 \x.M
          | Ap Term Term    -- 应用，如 M N
  deriving (Eq, Show)

data CurryType = Phi Char                   -- 基本类型，如 A、B
               | Arrow CurryType CurryType  -- 函数类型，如 A -> B
  deriving (Show, Eq)

-- 为了方便，我们为 Arrow 定义一个中缀运算符
(-->) :: CurryType -> CurryType -> CurryType
(-->) = Arrow

我们希望能够推出\x.x的类型是A -> A，\f.\g.\x.f (g x)的类型是(B -> C) -> (A -> B) -> A -> C等。

TIP

💡动手试一试：你能尝试用Haskell写一个函数验证类型是否正确吗？这比推导类型简单得多！

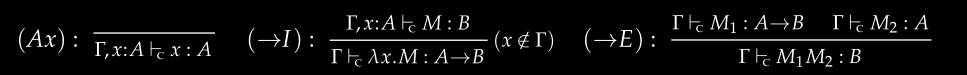
如何实现：从类型签名开始

我们将实现一个称为主偶算法的类型推导算法。它的定义如下：

如果你已经看懂了，那恭喜你，你也没有看下去的必要了（

不过大多数人第一次看都会一头雾水，没关系，我们一步一步来。

理解算法的输入和输出

算法返回一个包含上下文和推导出的类型的元组。上下文是一个映射表，记录每个变量的类型，我们可以用Haskell的Data.Map来表示。

由于算法需要不断生成新的类型变量（如 A、B、C...），我们需要维护一个状态来记录当前使用到了哪个字母。为了简单起见，我们假设字母 A 到 Z 足够使用。

data TypeCtx = TypeCtx
  { env :: Map Char CurryType,
    label :: Label
  }

定义主偶对（算法的返回结果）：

type PrincipalPair = (TypeCtx, CurryType)

好，现在我们可以把算法的类型写出来了：

emptyEnv :: TypeCtx
emptyEnv = TypeCtx Map.empty 'A'

pp :: Term -> PrincipalPair
-- 因为我们不能和定义里一样变出新类型名，我们得维护这个状态把它传来传去
pp = pp' emptyEnv
  where
    pp' :: TypeCtx -> Term -> PrincipalPair
    pp' = undefined -- 待实现

情况一：变量

实现式子是变量的情况：

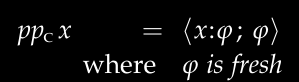
这里公式说：看到任意变量x，推导出类型a（任意新类型名），并告诉上下文x被映射到a。

pp' ctx (V c) =
  -- 记录“字母A已被使用”，现在可用字母是B
  let (a, ctx') = next ctx
   -- 记录“变量c的类型是A”
   in (add c a ctx', a)

这里的 next 函数负责生成新类型名，add 函数负责向上下文中添加新的变量-类型映射。

fresh :: Label -> Label
fresh = chr . (+ 1) . ord

next :: TypeCtx -> (CurryType, TypeCtx)
next (TypeCtx env l) = let l' = fresh l in (Phi l, TypeCtx env l')

add :: Char -> CurryType -> TypeCtx CurryType -> TypeCtx CurryType
add c ty (TypeCtx env l) = TypeCtx (Map.insert c ty env) l

情况二：抽象

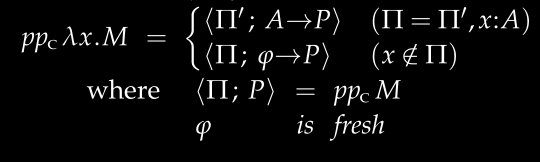
这个规则处理 Lambda 抽象 \x.M：

1. 首先推导 M 的类型 P
2. 检查上下文中是否已经知道 x 的类型：
   • 如果知道（比如 x 必须是 Int -> Int），则整个表达式的类型就是 x的类型 -> P
   • 如果不知道，就为 x 分配一个新类型 a，然后整个表达式的类型是 a -> P

pp' ctx (Ab x m) = 
  let (ctx', p) = pp' ctx m  -- 先推导 M 的类型
  in case env ctx' !? x of
    Just ty -> (ctx', ty --> p)  -- 如果已知 x 的类型
    Nothing -> 
      let (a, ctx'') = next ctx'  -- 否则创建新类型
      in (add x a ctx'', a --> p)

情况三：应用

实现式子是应用的情况：

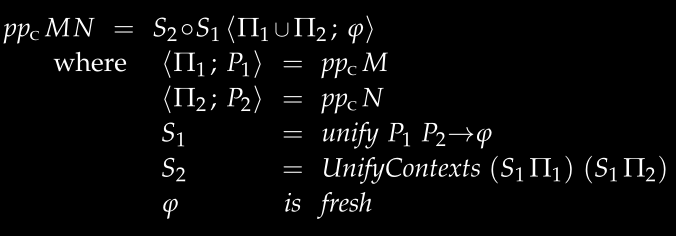
这是最复杂的情况，处理函数应用 M N：

1. 分别推导 M 和 N 的类型
2. 为了使应用成立，M 的类型必须是 N的类型 -> 某个新类型
3. 但之前我们给变量分配的类型是任意的，所以可能需要统一（unify） 这些类型

比如：推导f x的类型，递归给出f类型为A，x类型为B。这时候需要unify这个函数找出一个映射（把A替换成符合上下文的类型），使得被映射后M的类型可以被应用到N上，同时这个映射需要修改所有已知的上下文中的类型（UnifyContext）。

另一个例子，假设我们推导 (\x.x) y：

1. 推导 (\x.x) 得到：ctx1 = {x: A}, 类型 A -> A
2. 推导 y 得到：ctx2 = {x: A, y: B}, 类型 B

如果简单合并 ctx1 和 ctx2，可能会：

• 产生不一致的类型假设，导致逻辑错误
• 丢失信息（键可能冲突）

正确的做法：不应该简单合并，而应该通过类型统一来协调两个上下文。

这部分内容比较复杂，我们将在下一篇文章中详细讲解。

pp' ctx (Ap m n) = s2 . s1 $ (ctx1 `union` ctx3, a)
  where
    (ctx1, p1) = pp' ctx m
    (ctx2, p2) = pp' ctx1 n
    (a, ctx3) = next ctx2
    s1 = unify p1 (p2 --> a)
    s2 = unifyctx (s1 ctx1) (s1 ctx3)

unify :: CurryType -> CurryType -> (CurryType -> CurryType)
unifyctx :: TypeCtx -> TypeCtx -> (CurryType -> CurryType)

欲知后事如何，且听下回分解。

动动手，动动脑

问题1 给定 Lambda 项：\x.\y.x

• 写出推导的调用树
• 在推导过程中，上下文会如何变化？请按步骤写出每个阶段的上下文状态。

问题2 推导 \a.a 时，假设初始 Label = 'A'：

• 会生成哪些类型变量？
• 最终返回的 TypeCtx 中的 Label 是什么？

问题3 手动推导以下 Lambda 项的类型：

• \x.x（恒等函数）
• \x.\y.x（K 组合子）
• \x.\y.y（另一个常量函数）