Lambda calculus typer from scratch - Part 2

NOTE

Prerequisites: You need to be familiar with basic Haskell syntax, understand recursion and higher-order functions. For example, you should be able to implement functions like zipWith and map yourself.

Corresponding code: https://github.com/xiaoshihou514/xingli

Introduction

Last time we implemented the first two cases of type inference (variables and abstractions), but got stuck on the most complex application case. We need to figure out how to unify the types of functions and values in applications:

pp' ctx (Ap m n) = s2 . s1 $ (ctx1 `union` ctx3, a)
  where
    (ctx1, p1) = pp' ctx m
    (ctx2, p2) = pp' ctx1 n
    (a, ctx3) = next ctx2
    -- The key step!
    s1 = unify p1 (p2 --> a)
    s2 = unifyctx (s1 ctx1) (s1 ctx3)

Today, we're going to "unify" p1 and p2 --> a.

Type Unification

How do we "unify" two types? The idea is that we should substitute some type variables to make the two types equal. For example: for the expression f x, where f has type A and x has type B, we need to unify A and B -> C. The substitution rule here needs to replace A with B -> C, making A = B -> C.

TIP

💡 Give it a try: How to unify the following types?

p1	p2 --> a
B -> C	A
A -> B	C -> D
A	A -> B

The principal type algorithm defines it as follows:

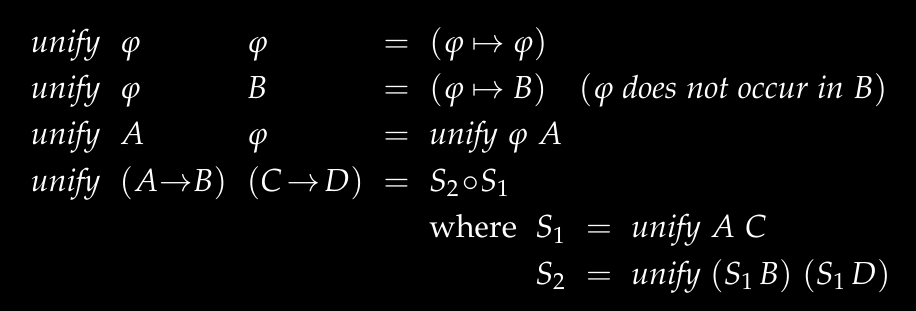
There are four cases in total. Here phi represents basic types (Int, String), and A, B represent arbitrary Curry types (which could be complex arrow types).

• Both sides are simple types and they are equal: no substitution needed, already the same
• Left side simple type, right side complex type: return a mapping that replaces the left side with the right side. If the left side appears in the right side type, then unification is impossible (e.g., A = A -> B obviously doesn't hold regardless of your substitutions).
• Right side simple type, left side complex type: same as above.
• Both sides are arrow types: first recursively try to unify A and C, modify B and D with that map, then try to unify B and D. The final mapping is the composition of the two maps.

So we can write:

unify :: CurryType -> CurryType -> (CurryType -> CurryType)
unify left right
  -- Both sides equal
  | (Phi p1) <- left, (Phi p2) <- right, p1 == p2 = id
  -- Left simple right complex, and left does not occur in right
  | (Phi p) <- left, p `notOccur` right =
      -- Define substitution mapping, replace all p with right
      let subst ty = case ty of
            Phi _ -> if ty == left then right else ty
            Arrow a b -> Arrow (subst a) (subst b)
       in subst
  -- Left complex right simple
  | (Phi _) <- right = unify right left
  -- Both sides complex
  | (Arrow a b) <- left,
    (Arrow c d) <- right =
      let s1 = unify a c            -- First unify A, C
          s2 = unify (s1 b) (s1 d)  -- Modify B, D according to substitution, then unify
       in s2 . s1                   -- Compose the two mappings
  | otherwise = error $ "Cannot unify " ++ prettyCT left ++ " and " ++ prettyCT right

Define notOccur as follows:

notOccur :: Label -> CurryType -> Bool
notOccur p (Phi a) = p /= a
notOccur p (Arrow a b) = p `notOccur` a && p `notOccur` b

Context Unification

The contexts from both sides might also conflict. Consider xy(xz), where the types of x on both sides are clearly different (y and z cannot be equal according to our previous logic, so the input types of the two x's must be different). We need to unify the variable descriptions from both contexts.

Context unification uses the previously defined unify function. It means that if a variable x is defined in both contexts, then all such x's need to be unified, and the final map is all these maps composed.

The Haskell code here might be a bit complex, try to see if you can understand it!

unifyctx :: TypeCtx -> TypeCtx -> (PrincipalPair -> PrincipalPair)
unifyctx ctx1 ctx2 = liftPP $ foldr (.) id subs
  where
    subs = [unify a b | (x, a) <- Map.toList env1, b <- maybeToList $ Map.lookup x env2]
    env1 = env ctx1
    env2 = env ctx2

liftPP :: (CurryType -> CurryType) -> (PrincipalPair -> PrincipalPair)
liftPP f (TypeCtx env l, a) = (TypeCtx (Map.map f env) l, f a)

First, we get all variables that are defined in both contexts and find their correction mappings:

env1 = env ctx1
env2 = env ctx2
subs = [unify a b |
    (x, a) <- Map.toList env1,
    -- <- cannot extract values from Maybe, so convert it to a list
    b <- maybeToList $ Map.lookup x env2
]

Use foldr to compose all mappings:

foldr (.) id subs

The mapping we get now can only correct one type. To apply it to the entire context, define a helper to map it over the Map.

liftPP :: (CurryType -> CurryType) -> (PrincipalPair -> PrincipalPair)
liftPP f (TypeCtx env l, a) = (TypeCtx (Map.map f env) l, f a)

The end...?

Now we can complete the last case of the principal type algorithm

-- Just lifted s1, everything else unchanged
pp' ctx (Ap m n) = s2 . liftPP s1 $ (ctx1 `union` ctx3, a)
  where
    -- First recursively derive the function
    (ctx1, p1) = pp' ctx m
    -- Recursively derive the input
    (ctx2, p2) = pp' ctx1 n
    -- Unify the two types
    (a, ctx3) = next ctx2
    s1 = unify p1 (p2 --> a)
    -- Unify the types in the contexts
    s2 = unifyctx (s1 ctx1) (s1 ctx3)

A concrete example: Deriving the type of (\x.x) y

1. Derive (\x.x): get {x: A}, type A -> A
2. Derive y: get {x: A, y: B}, type B
3. New type variable: C
4. Unify A->A and B->C:
   • Unify A and B: map A to B
   • Unify A and C: but A is already B, so unify B and C, map B to C
   • Final: A↦C, B↦C
5. After applying substitution: type is C, context is {x: C, y: C}

That's all of the algorithm stuff, let's learn some Haskell now.

Refactoring

Notice that we directly throw errors in unify, which isn't ideal because we claim in our types that we can infer the type of any Lambda term, but sometimes we can't (try deriving the type of \x.(x x) \x.(x x)).

In Haskell, the simplest solution is to return a Maybe, clearly indicating that type inference might fail:

unify :: CurryType -> CurryType -> Maybe (CurryType -> CurryType)
unify left right
  -- Just add Just to the first few cases
  | (Phi p1) <- left, (Phi p2) <- right, p1 == p2 = Just id
  | (Phi p) <- left, p `notOccur` right =
      let subst ty = case ty of
            Phi _ -> if ty == left then right else ty
            Arrow a b -> Arrow (subst a) (subst b)
       in Just subst
  | (Phi _) <- right = unify right left
  -- Here we use do syntax to chain Maybe handling
  | (Arrow a b) <- left,
    (Arrow c d) <- right = do
      s1 <- unify a c           -- If fails, directly return Nothing
      s2 <- unify (s1 b) (s1 d) -- Same as above
      return $ s2 . s1          -- return = Just
  | otherwise = Nothing

pp :: Term -> PrincipalPair
pp :: Term -> Maybe PrincipalPair
pp = pp' emptyEnv
  where
    pp' :: TypeCtx -> Term -> PrincipalPair
    pp' :: TypeCtx -> Term -> Maybe PrincipalPair
    pp' = ...

Here we use do syntax. Effectively, x <- ... "unwraps" the Maybe; if it's a Nothing, it "early returns" a Nothing; otherwise, it extracts the value. Since next always succeeds (doesn't return Maybe), we use let syntax to indicate no unwrapping is needed. The final return is equivalent to wrapping with Just (part of Monad definition of Maybe).

We also need to modify the upper-level code:

Since the first three cases always succeed, we just need to add a Just to satisfy the type constraint.

pp' :: TypeCtx -> Term -> Maybe PrincipalPair
pp' ctx (V c) =
  let (a, ctx') = next ctx
   in (add c a ctx', a)
   in Just (add c a ctx', a)
pp' ctx (Ab x m) = do
  (ctx', p) <- pp' ctx m
  case env ctx' !? x of
    Just ty -> Just (ctx', ty --> p)
    Nothing ->
      let (a, ctx'') = next ctx'
      in (add x a ctx'', a --> p)
      in Just (add x a ctx'', a --> p)

For the last case, we use do syntax again:

pp' ctx (Ap m n) = s2 . liftPP s1 $ (ctx1 `union` ctx3, a)
  where
    (ctx1, p1) = pp' ctx m 
    (ctx2, p2) = pp' ctx1 n 
    (a, ctx3) = next ctx2 
    s1 = unify p1 (p2 --> a)
    s2 = unifyctx (s1 ctx1) (s1 ctx3)
pp' ctx (Ap m n) = do
  (ctx1, p1) <- pp' ctx m 
  (ctx2, p2) <- pp' ctx1 n 
  let (a, ctx3) = next ctx2 
  s1 <- unify p1 (p2 --> a)
  s2 <- unifyctx (apply s1 ctx1) (apply s1 ctx3)
  return $ s2 . liftPP s1 $ (ctx1 `union` ctx3, a)

Finally we modify unifyctx:

subs :: [Maybe (CurryType -> CurryType)]
unifyctx ctx1 ctx2 = liftPP . foldr (.) id subs 
unifyctx ctx1 ctx2 = liftPP . foldr (.) id <$> sequence subs 

Here <$> is just fmap (recall what does fmap do to a Maybe?)

f <$> maybe = fmap f maybe

sequence is more subtle, so its type is:

sequence :: (Traversable t, Monad m) => t (m a) -> m (t a)
-- Specific type: t = [a], m = Maybe
sequence :: [Maybe (... -> ...)] -> Maybe [... -> ...]

That is, if there's a Nothing in the list (one failure), return Nothing for the whole list (fail all). If not, return Just [...], which is exactly what we need.

Give it a shot

Q1 Manually derive the type of (\x.\y.x) (\z.z):

• Write out the context and type at each derivation step
• What are the substitution mappings for each type unification?

Q2 Why can't we derive the type of \x.(x x)? Try to manually derive it and find where the problem occurs.

Q3 Thought question: We cannot derive all fixed-point combinators (because they all have self-application, and A and A -> A cannot be unified). We rely on fixed-point combinators to express recursion, so we currently cannot derive types for recursive functions. How can we solve this problem?

---

Congratulations! You now understand a complete type inference algorithm.

Complete code reference: GitHub Repository

Of course, this is just the simplest type system :)

If you want to know how to derive more complex cases (how to derive where? how to derive recursive functions?), you can read my next blog post. We will gradually introduce more concepts to make Lambda terms capable of expressing any expression in Haskell.