手把手教你ML类型推导，C++老登要长脑子了

本文我们将系统介绍ML语言中的类型推导，重点解析W算法的实现原理。

ML表达式的定义

data MLTerm where
  V :: String -> MLTerm
  Const :: String -> MLTerm
  Ab :: String -> MLTerm -> MLTerm
  Ap :: MLTerm -> MLTerm -> MLTerm
  Let :: (String, MLTerm) -> MLTerm -> MLTerm
  Fix :: String -> MLTerm -> MLTerm
  deriving (Eq, Show)

相较于LCNR系统，ML表达式增加了常量（Const）和Let绑定。Let绑定类似于LCNR中的赋值操作，Fix则对应LCNR的LetRec。常量表示编程语言中的字面量，如整数、字符串、浮点数等。

ML类型的定义

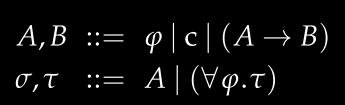
ML类型系统是许多编程语言类型系统的基础，因此我们需要正确定义基本类型和多态类型。ML中的多态类型通过类型变量实现，类型可以是类型变量或基本类型（如Int、String），并可通过箭头组合成函数类型。

注意：forall量词必须出现在类型的最外层。像forall a.a -> (forall b.b -> b)这样的类型在ML中是不允许的。允许forall在任意位置出现的类型系统被称为F系统（System F），该系统虽然更强大，但已被证明无法进行类型推导。

data MLType
  = -- 类型变量
    Phi Char
  | -- 基本类型：Int, String...
    Basic String
  | Arrow MLType MLType
  | -- 为简洁起见，此处不强制要求量词位于顶层
    Qtf Char MLType
  deriving (Show, Eq)

ML系统中的类型替换

ML系统的类型替换需要处理从柯里类型到ML类型变量的映射，同时还需定义类型变量到基本类型的替换规则。

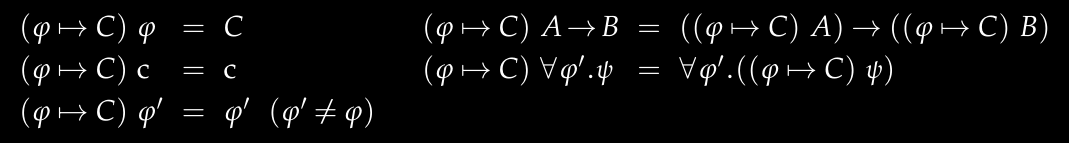
ML系统中的类型统一

类似地，ML系统中的类型统一算法需要考虑基本类型的情况：

W算法的实现

首先注意W算法相较于之前的算法多了一个参数v，这是一个映射表，用于确定常量的类型。因此我们定义Env类型如下：

type PrincipalPair = (MLType -> MLType, MLType)
type Env = Map String MLType

algorithmW :: Env -> MLTerm -> Maybe MLType
algorithmW v term_ = snd . snd <$> algorithmW' emptyCtx term_
  where
    algorithmW' :: TypeCtx -> MLTerm -> Maybe (TypeCtx, PrincipalPair)

与之前类似，我们需要传递TypeCtx，而Env作为静态环境可直接捕获。

常量类型的推导

对于常量（如1、"foo"、[1, 2, 3]），我们直接从环境中获取其类型。例如，1的类型为Int，字符串的类型为String等。需要注意的是，这些类型可能是多态的，例如id的类型为forall a.a -> a。

algorithmW' ctx (Const s) = do
  a <- v !? s
  let (ctx', b) = freshInstance (ctx, a)
  return (ctx', (id, b))

为避免与现有类型变量冲突，我们需要通过freshInstance函数生成新实例：

freshInstance :: (TypeCtx, MLType) -> (TypeCtx, MLType)
freshInstance = snd . freshInstance' Map.empty
  where
    freshInstance' ::
      Map Char MLType ->
      (TypeCtx, MLType) ->
      (Map Char MLType, (TypeCtx, MLType))
    -- 仅替换非自由类型变量
    freshInstance' env (ctx, Qtf c ty) =
      let (freshTy, ctx') = next ctx
          env' = Map.insert c freshTy env
       in freshInstance' env' (ctx', ty)
    -- 自由类型变量保持不变
    freshInstance' env (ctx, Phi c) =
      case Map.lookup c env of
        Just ty -> (env, (ctx, ty))
        Nothing -> (env, (ctx, Phi c))
    freshInstance' env (ctx, Arrow left right) =
      let (env', (ctx', left')) = freshInstance' env (ctx, left)
          (env'', (ctx'', right')) = freshInstance' env' (ctx', right)
       in (env'', (ctx'', Arrow left' right'))
    freshInstance' env x = (env, x)

看到这里你可能会很奇怪：类型变量还能不被量化吗？

可以的兄弟，可以的。其实仔细想一下这是很合理的，我们提到ML类型只允许forall出现在顶层，那么推导的过程中我们需要带着没被量化的类型到处跑，最后统一进行量化。

那么何时进行量化呢？通常是在推导到达顶层、不再需要进一步替换时。观察发现，唯一添加量化的位置是Let表达式（对应$\overline{S_1\mathrm{\Gamma }}A$）。可以认为Let表达式限定了其类型的抽象程度。

变量类型的推导

对于变量，直接从上下文中读取其类型并进行替换：

algorithmW' ctx (V c) = do
  a <- env ctx !? c
  let (ctx', b) = freshInstance (ctx, a)
  return (ctx', (id, b))

抽象类型的推导

algorithmW' ctx (Ab x e) = do
  let (phi, ctx') = next ctx
  (ctx'', (s, a)) <- algorithmW' (add x phi ctx') e
  return (ctx'', (s, s (phi --> a)))

Let表达式的类型推导

Let表达式是ML的新语法结构，其效果类似于LCNR中的赋值操作。我们首先推导绑定值的类型，然后将其量化后用于后续表达式的推导：

algorithmW' ctx (Let (x, e1) e2) = do
  (TypeCtx _ l, (s1, a)) <- algorithmW' ctx e1
  let (TypeCtx mapping _) = apply s1 ctx
  let ctx'' = TypeCtx mapping l
  let sigma = generalize ctx'' a
  (ctx''', (s2, b)) <- algorithmW' (add x sigma ctx'') e2
  return (ctx''', (s2 . s1, b))

generalize :: TypeCtx -> MLType -> MLType

其中generalize函数的作用是对所有不在上下文中的类型变量添加forall量词：

generalize :: TypeCtx -> MLType -> MLType
generalize ctx ty = Set.foldl (\f -> (f .) . Qtf) id (fvty \\ fvctx) ty
  where
    fvctx :: Set Char
    fvctx = Set.unions $ map (free . snd) $ Map.toList (env ctx)

    fvty :: Set Char
    fvty = free ty

    free :: MLType -> Set Char
    free = free' Set.empty
      where
        free' :: Set Char -> MLType -> Set Char
        free' env (Qtf c t) = free' (Set.insert c env) t
        free' env (Phi c)
          | c `elem` env = Set.empty
          | otherwise = Set.fromList [c]
        free' env (Arrow l r) = Set.union (free' env l) (free' env r)
        free' _ (Basic _) = Set.empty

这里可能有疑问：添加和移除forall量词的实际意义是什么？实际上，当类型被forall限定时，相当于将其"冻结"为多态类型变量。必须去除forall并替换为新的类型变量后，才能进一步替换为具体类型。在实际的Haskell实现中，这一过程可能显得冗余，可以考虑优化（如使用更高效的J算法），但作为定义的一部分，我们仍保留此机制。

递归表达式的类型推导

对于递归表达式，我们采用与LCNR类似的方法：先为递归标识符赋予一个类型变量，推导完成后再进行统一：

algorithmW' ctx (Fix g e) = do
  let (phi, ctx') = next ctx
  (ctx'', (s1, a)) <- algorithmW' (add g phi ctx') e
  s2 <- unify (s1 phi) a
  return (ctx'', (s2 . s1, s2 a))

应用表达式的类型推导

应用表达式的推导与LCNR类似：分别推导函数和参数的类型，然后确保函数类型能够接受参数类型：

algorithmW' ctx (Ap e1 e2) = do
  (ctx', (s1, a)) <- algorithmW' ctx e1
  (ctx'', (s2, b)) <- algorithmW' (apply s1 ctx') e2
  let (phi, ctx''') = next ctx''
  s3 <- unify (s2 a) (b --> phi)
  return (ctx''', (s3 . s2 . s1, s3 phi))

结语

W算法作为ML类型系统的核心推导算法，通过优雅地处理多态类型、Let绑定和递归等语言特性，展现了类型推导理论的深度与美感。该算法不仅在理论上有重要意义，也为实际编程语言（如Haskell、OCaml等）的类型系统实现提供了坚实基础。

ML系统还是不支持相互递归，不过可以通过一些扩展支持，然后在实现中做一些分析简化情况等等。LCNR通过扩展也可以支持相互递归，不过那个实现被证明无法做类型推导，需要用户提示一些类型。