Lambda calculus typer from scratch - ML and algorithm W

This article systematically introduces type inference in the ML language, with a focus on explaining the implementation principles of the W algorithm.

Definition of ML Expressions

data MLTerm where
  V :: String -> MLTerm
  Const :: String -> MLTerm
  Ab :: String -> MLTerm -> MLTerm
  Ap :: MLTerm -> MLTerm -> MLTerm
  Let :: (String, MLTerm) -> MLTerm -> MLTerm
  Fix :: String -> MLTerm -> MLTerm
  deriving (Eq, Show)

Compared to the LCNR system, ML expressions add constants (Const) and Let bindings. Let bindings are similar to assignment operations in LCNR, while Fix corresponds to LetRec in LCNR. Constants represent literals in programming languages, such as integers, strings, floating-point numbers, etc.

Definition of ML Types

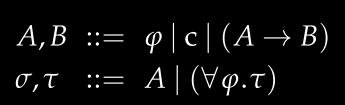
The ML type system forms the basis of type systems in many programming languages. Therefore, we need to correctly define basic types and polymorphic types. Polymorphic types in ML are implemented through type variables. A type can be either a type variable or a basic type (such as Int, String) and can be combined into function types via arrows.

Note: The forall quantifier must appear at the outermost level of a type. Types like forall a.a -> (forall b.b -> b) are not allowed in ML. Type systems that allow forall to appear anywhere are known as System F, which, although more powerful, have been proven incapable of full type inference.

data MLType
  = -- Type variable
    Phi Char
  | -- Basic types: Int, String...
    Basic String
  | Arrow MLType MLType
  | -- For brevity, we do not enforce the quantifier to be at the top level here
    Qtf Char MLType
  deriving (Show, Eq)

Type Substitution in the ML System

Type substitution in the ML system needs to handle mappings from Curry types to ML type variables, while also defining substitution rules for type variables to basic types.

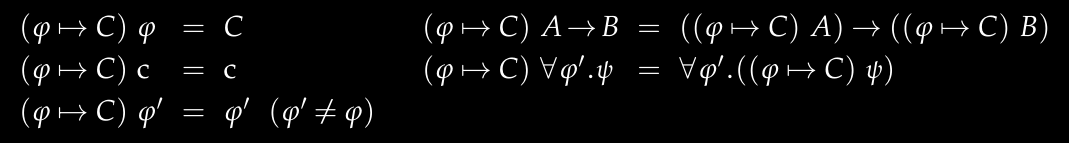
Type Unification in the ML System

Similarly, the type unification algorithm in the ML system must account for basic types:

Implementation of the W Algorithm

First, note that the W algorithm includes an additional parameter v compared to previous algorithms. This is a mapping table used to determine the types of constants. Thus, we define the Env type as follows:

type PrincipalPair = (MLType -> MLType, MLType)
type Env = Map String MLType

algorithmW :: Env -> MLTerm -> Maybe MLType
algorithmW v term_ = snd . snd <$> algorithmW' emptyCtx term_
  where
    algorithmW' :: TypeCtx -> MLTerm -> Maybe (TypeCtx, PrincipalPair)

Similar to before, we need to pass the TypeCtx, while Env can be captured directly as a static environment.

Type Inference for Constants

For constants (such as 1, "foo", [1, 2, 3]), we directly retrieve their types from the environment. For example, the type of 1 is Int, the type of a string is String, etc. Note that these types may be polymorphic; for instance, the type of id is forall a.a -> a.

algorithmW' ctx (Const s) = do
  a <- v !? s
  let (ctx', b) = freshInstance (ctx, a)
  return (ctx', (id, b))

To avoid conflicts with existing type variables, we generate new instances via the freshInstance function:

freshInstance :: (TypeCtx, MLType) -> (TypeCtx, MLType)
freshInstance = snd . freshInstance' Map.empty
  where
    freshInstance' ::
      Map Char MLType ->
      (TypeCtx, MLType) ->
      (Map Char MLType, (TypeCtx, MLType))
    -- Only replace non-free type variables
    freshInstance' env (ctx, Qtf c ty) =
      let (freshTy, ctx') = next ctx
          env' = Map.insert c freshTy env
       in freshInstance' env' (ctx', ty)
    -- Free type variables remain unchanged
    freshInstance' env (ctx, Phi c) =
      case Map.lookup c env of
        Just ty -> (env, (ctx, ty))
        Nothing -> (env, (ctx, Phi c))
    freshInstance' env (ctx, Arrow left right) =
      let (env', (ctx', left')) = freshInstance' env (ctx, left)
          (env'', (ctx'', right')) = freshInstance' env' (ctx', right)
       in (env'', (ctx'', Arrow left' right'))
    freshInstance' env x = (env, x)

At this point, you might wonder: Can type variables remain unquantified?

Indeed, it is possible. Upon careful consideration, this is quite reasonable. Since ML types only allow forall at the outermost level, during the inference process we need to carry unquantified type variables and perform quantification uniformly at the end.

So when does quantification occur? Typically, it happens when inference reaches the top level and no further substitution is needed. Observation reveals that the only place where quantification is added is in Let expressions (corresponding to $\overline{S_1\mathrm{\Gamma }}A$). It can be said that Let expressions limit the abstraction level of their types.

Type Inference for Variables

For variables, we directly read their types from the context and perform substitution:

algorithmW' ctx (V c) = do
  a <- env ctx !? c
  let (ctx', b) = freshInstance (ctx, a)
  return (ctx', (id, b))

Type Inference for Abstractions

algorithmW' ctx (Ab x e) = do
  let (phi, ctx') = next ctx
  (ctx'', (s, a)) <- algorithmW' (add x phi ctx') e
  return (ctx'', (s, s (phi --> a)))

Type Inference for Let Expressions

Let expressions are a new syntactic construct in ML, with effects similar to assignment operations in LCNR. We first infer the type of the bound value, then quantify it for use in the subsequent expression:

algorithmW' ctx (Let (x, e1) e2) = do
  (TypeCtx _ l, (s1, a)) <- algorithmW' ctx e1
  let (TypeCtx mapping _) = apply s1 ctx
  let ctx'' = TypeCtx mapping l
  let sigma = generalize ctx'' a
  (ctx''', (s2, b)) <- algorithmW' (add x sigma ctx'') e2
  return (ctx''', (s2 . s1, b))

generalize :: TypeCtx -> MLType -> MLType

Here, the generalize function adds a forall quantifier to all type variables not present in the context:

generalize :: TypeCtx -> MLType -> MLType
generalize ctx ty = Set.foldl (\f -> (f .) . Qtf) id (fvty \\ fvctx) ty
  where
    fvctx :: Set Char
    fvctx = Set.unions $ map (free . snd) $ Map.toList (env ctx)

    fvty :: Set Char
    fvty = free ty

    free :: MLType -> Set Char
    free = free' Set.empty
      where
        free' :: Set Char -> MLType -> Set Char
        free' env (Qtf c t) = free' (Set.insert c env) t
        free' env (Phi c)
          | c `elem` env = Set.empty
          | otherwise = Set.fromList [c]
        free' env (Arrow l r) = Set.union (free' env l) (free' env r)
        free' _ (Basic _) = Set.empty

A question may arise here: What is the practical significance of adding and removing forall quantifiers? In practice, when a type is bound by forall, it is effectively "frozen" as a polymorphic type variable. The forall must be removed and replaced with a new type variable before it can be further substituted with a concrete type. In actual Haskell implementations, this process may seem redundant and could be optimized (for example, by using the more efficient J algorithm). However, as part of the definition, we retain this mechanism.

Type Inference for Recursive Expressions

For recursive expressions, we adopt a method similar to LCNR: first assign a type variable to the recursive identifier, then unify after inference is complete:

algorithmW' ctx (Fix g e) = do
  let (phi, ctx') = next ctx
  (ctx'', (s1, a)) <- algorithmW' (add g phi ctx') e
  s2 <- unify (s1 phi) a
  return (ctx'', (s2 . s1, s2 a))

Type Inference for Application Expressions

The inference for application expressions is similar to LCNR: infer the types of the function and argument separately, then ensure the function type can accept the argument type:

algorithmW' ctx (Ap e1 e2) = do
  (ctx', (s1, a)) <- algorithmW' ctx e1
  (ctx'', (s2, b)) <- algorithmW' (apply s1 ctx') e2
  let (phi, ctx''') = next ctx''
  s3 <- unify (s2 a) (b --> phi)
  return (ctx''', (s3 . s2 . s1, s3 phi))

Conclusion

As the core inference algorithm of the ML type system, the W algorithm demonstrates the depth and elegance of type inference theory by gracefully handling language features such as polymorphic types, Let bindings, and recursion. This algorithm holds significant theoretical importance and provides a solid foundation for implementing type systems in practical programming languages (such as Haskell and OCaml).

The ML system still does not support mutual recursion, although it can be extended to do so, with some analysis and simplification in the implementation. LCNR can also support mutual recursion through extensions, but that implementation has been proven incapable of type inference without user-provided type hints.