手把手教你Lambda式类型推导(赋值与递归篇):C++老登的痛苦救赎
引言
在掌握了基础Lambda表达式类型推导之后,我们迎来了两个更加实用的扩展功能:赋值与递归。这两个特性能让我们的类型系统真正具备实用价值,让代码组织变得更加清晰高效。
赋值:为表达式命名
在实际编程中,我们经常需要为特定表达式命名以便重复使用。这不仅提高了代码的可读性,还避免了重复的类型推导工作。为此我们定义了新的语言
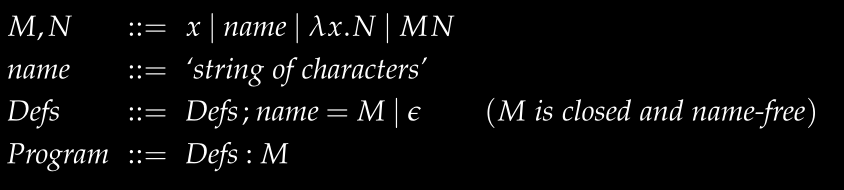
看个具体例子:
id = \x.x
id id类型推导的核心思路
推导带赋值的表达式类型时,基本逻辑与原生Lambda表达式一致,关键在于维护一个环境映射表来记录已定义的符号及其类型。
haskell
type Env = Map String CurryType
ppln :: LCNProgram -> Maybe PrincipalPair
ppln (LCNProgram defs main) = do
env <- buildEnv defs -- 构建初始环境
ppln' main env emptyEnv -- 在主表达式中使用该环境环境构建过程就是顺序推导每个绑定的类型:
haskell
buildEnv :: [Def] -> Maybe Env
buildEnv = foldr buildEnv' (Just Map.empty)
where
buildEnv' :: Def -> Maybe Env -> Maybe Env
buildEnv' (Def name m) env = do
(_, a) <- ppln' m Map.empty emptyEnv
Map.insert name a <$> env遇到已定义符号时,直接从环境中查询其类型:
haskell
ppln' (Name n) e ctx = do
ty <- e !? n -- 环境查找
return $ freshInstance ctx ty这里为什么要用freshInstance?因为环境中的类型是用初始标签推导的,这些标签可能已经被使用过。我们需要生成新的类型副本来避免冲突。
haskell
freshInstance :: TypeCtx -> CurryType -> PrincipalPair
freshInstance = (fst .) . freshInstance' Map.empty
where
freshInstance' ::
Map Char CurryType ->
TypeCtx ->
CurryType ->
(PrincipalPair, Map Char CurryType)
-- 具体实现处理类型变量和函数类型
递归:让函数自我调用
递归是函数式编程的核心特性之一,但它的类型推导相对复杂。核心思路是:为递归符号预设一个初始类型,在推导过程中逐步细化这个类型。

具体实现时需要扩展环境的概念,记录哪些符号是递归定义的:
haskell
type Env = Map String (CurryType, Bool) -- 增加布尔标记表示是否为递归
buildEnv :: TypeCtx -> [Def] -> Maybe (TypeCtx, Env)
buildEnv c = foldl (flip buildEnv') $ Just (c, emptyEnv)
where
buildEnv' :: Def -> Maybe (TypeCtx, Env) -> Maybe (TypeCtx, Env)
buildEnv' (Def name m) macc = do
(ctx, env) <- macc
(ctx', a, env') <- ppln' m env ctx
return (ctx', addEnv name a env') -- 非递归情况直接添加
buildEnv' (RecDef name m) macc = do
(ctx, env) <- macc
-- 关键步骤:为递归函数创建初始类型占位符
let (phi, ctx') = next ctx
-- 在包含递归绑定的环境中推导函数体
(ctx'', a, env') <- ppln' m (addEnvRec name phi env) ctx'
-- 从环境中获取递归函数的实际推导类型
(b, True) <- env' !? name
-- 统一预期类型与实际类型
s <- unify a b
-- 最终确定递归函数类型
return (ctx'', addEnvRec name (s a) env)这个算法巧妙之处在于:它先给递归函数一个"临时类型",让函数体能够正常推导,最后通过类型统一来验证和确定最终类型。
结语
通过赋值和递归的引入,我们的类型系统已经具备了处理现实编程需求的能力。虽然推导过程变得更加复杂,但核心的HM类型系统框架依然清晰可靠。掌握这些进阶技巧,你将能更好地理解现代函数式语言类型系统的工作原理。
值得注意的是,