Lambda calculus typer from scratch - bindings and recursion

Introduction

Having looked at the fundamentals of lambda expression type inference, we now move on to two more practical extensions: assignment and recursion. These features empower our type system to become truly practical, making code organization clearer and more efficient.

Assignment: Naming Expressions

In practical programming, we often need to name specific expressions for reuse. This not only improves code readability but also avoids redundant type inference work. To this end, we define a new language, ${\mathrm{\Lambda }}_N$:

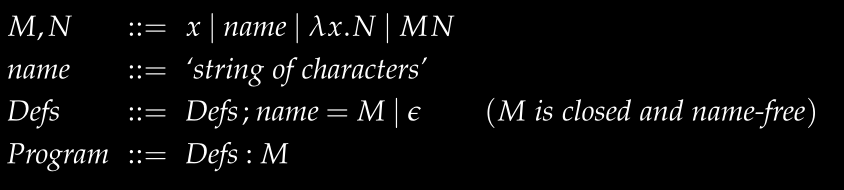
Consider a specific example:

id = \x.x
id id

The Core Idea of Type Inference

When inferring types for expressions with assignments, the basic logic aligns with that of raw lambda expressions. The key is maintaining an environment mapping to record defined symbols and their types.

type Env = Map String CurryType

ppln :: LCNProgram -> Maybe PrincipalPair
ppln (LCNProgram defs main) = do
  env <- buildEnv defs        -- Build the initial environment
  ppln' main env emptyEnv     -- Use this environment in the main expression

The environment building process involves sequentially inferring the type for each binding:

buildEnv :: [Def] -> Maybe Env
buildEnv = foldr buildEnv' (Just Map.empty)
  where
    buildEnv' :: Def -> Maybe Env -> Maybe Env
    buildEnv' (Def name m) env = do
      (_, a) <- ppln' m Map.empty emptyEnv
      Map.insert name a <$> env

When encountering a defined symbol, its type is directly queried from the environment:

ppln' (Name n) e ctx = do
  ty <- e !? n  -- Environment lookup
  return $ freshInstance ctx ty

Why use freshInstance here? Because the types in the environment are inferred with initial labels, and these labels may have already been used. We need to generate a new copy of the type to avoid conflicts.

freshInstance :: TypeCtx -> CurryType -> PrincipalPair
freshInstance = (fst .) . freshInstance' Map.empty
  where
    freshInstance' ::
      Map Char CurryType ->
      TypeCtx ->
      CurryType ->
      (PrincipalPair, Map Char CurryType)
    -- Implementation details handle type variables and function types

Recursion: Self-Calling Functions

Recursion is a core feature of functional programming, but its type inference is relatively more complex. The core idea is: assign a recursive symbol an initial type, and gradually refine this type during inference.

The implementation requires extending the concept of the environment to record which symbols are recursively defined:

type Env = Map String (CurryType, Bool)  -- Add a Boolean flag for recursion

buildEnv :: TypeCtx -> [Def] -> Maybe (TypeCtx, Env)
buildEnv c = foldl (flip buildEnv') $ Just (c, emptyEnv)
  where
    buildEnv' :: Def -> Maybe (TypeCtx, Env) -> Maybe (TypeCtx, Env)
    buildEnv' (Def name m) macc = do
      (ctx, env) <- macc
      (ctx', a, env') <- ppln' m env ctx
      return (ctx', addEnv name a env')  -- Direct addition for non-recursive case
    
    buildEnv' (RecDef name m) macc = do
      (ctx, env) <- macc
      -- Key step: create an initial type placeholder for the recursive function
      let (phi, ctx') = next ctx
      -- Derive the function body in an environment containing the recursive binding
      (ctx'', a, env') <- ppln' m (addEnvRec name phi env) ctx'
      -- Retrieve the actual derived type of the recursive function from the environment
      (b, True) <- env' !? name
      -- Unify the expected type with the actual type
      s <- unify a b
      -- Finalize the type of the recursive function
      return (ctx'', addEnvRec name (s a) env)

The cleverness of this algorithm lies in: first giving the recursive function a "temporary type" so that the function body can be inferred normally, and finally verifying and determining the final type through type unification.

Conclusion

With the introduction of assignment and recursion, our type system now has the capability to handle real-world programming needs. Although the inference process has become more complex, the core HM type system framework remains clear and reliable. Mastering these advanced techniques will enable you to better understand how type systems in modern functional languages work.

It is worth noting that the ${\mathrm{\Lambda }}_{NR}$ system still has many limitations, though we haven't mentioned them. This type system still theoretically does not allow polymorphism (even though the type inference algorithm achieves a similar effect). In the next blog post, we will introduce polymorphism through the ML type system—a more elegant type system built upon ${\mathrm{\Lambda }}_N$ and ${\mathrm{\Lambda }}_{NR}$ by Hindley Milner. It is a milestone in the type systems of functional programming.